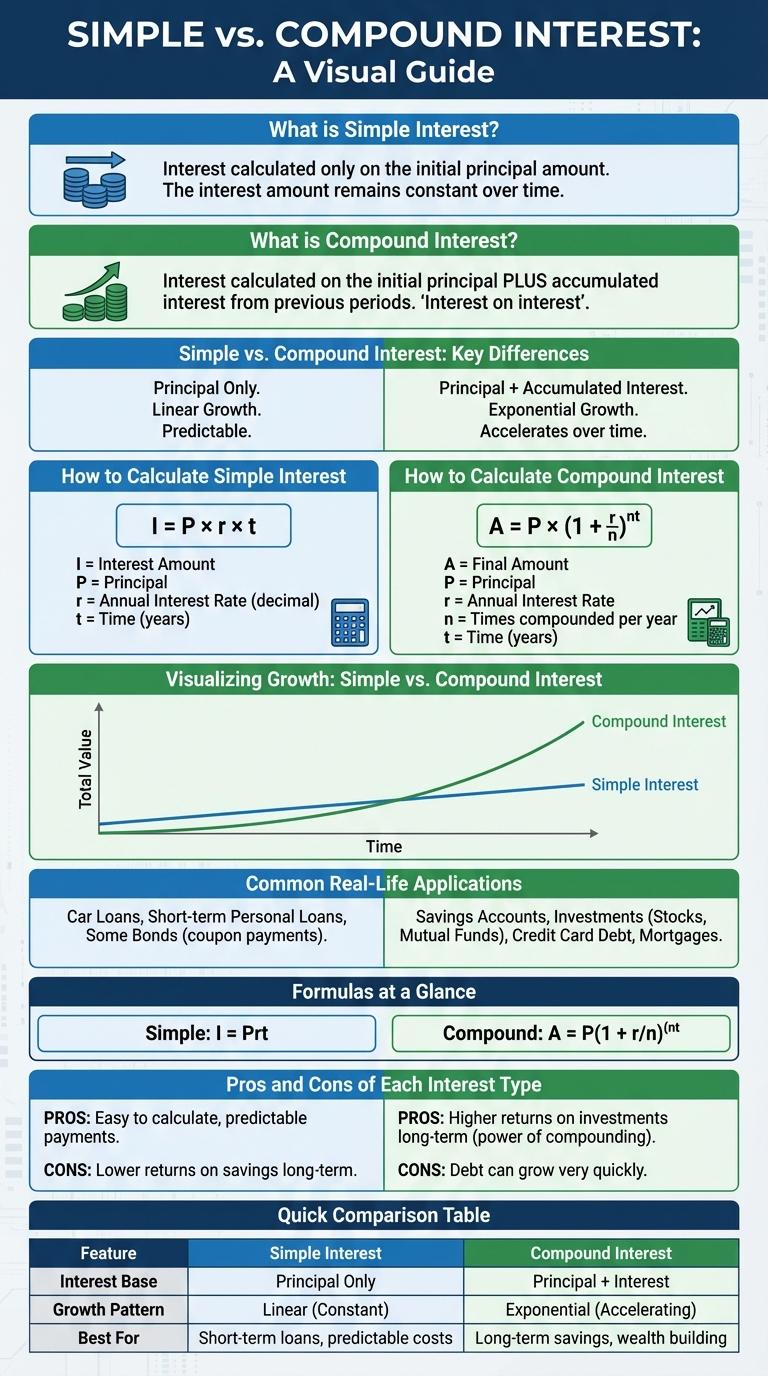
Simple interest calculates earnings based on the original principal only, making it straightforward and easy to understand. Compound interest grows faster by adding accumulated interest to the principal, resulting in exponential growth over time. Visualizing these differences through an infographic highlights the impact of interest types on savings and investments.
What is Simple Interest?
Simple interest is a calculation of interest charged only on the original principal amount of a loan or investment. The formula for simple interest is I = P x R x T, where I is the interest, P is the principal, R is the annual interest rate, and T is the time in years. Simple interest does not take into account the interest earned on previously accumulated interest, making it straightforward and easy to calculate.
What is Compound Interest?
Compound interest is the interest calculated on the initial principal and also on the accumulated interest from previous periods. It differs from simple interest, which is only calculated on the principal amount.
Compound interest allows investments to grow faster because interest earns interest over time. It is commonly used in savings accounts, loans, and investments to maximize returns. The formula for compound interest is A = P(1 + r/n)^(nt), where interest compounds n times per year.
Simple vs. Compound Interest: Key Differences
What are the key differences between simple and compound interest? Simple interest is calculated only on the initial principal, while compound interest is calculated on the principal plus accumulated interest. Compound interest typically results in higher returns over time due to interest-on-interest growth.
How to Calculate Simple Interest
Simple interest is calculated using the formula: Interest = Principal x Rate x Time. It applies a fixed percentage of the principal amount over a specific period.
The principal is the initial amount of money invested or borrowed. The rate is the annual interest rate, expressed as a decimal, and time is measured in years.
How to Calculate Compound Interest
| Interest Type | Calculation Method |
|---|---|
| Simple Interest | Principal x Rate x Time |
| Compound Interest | Principal x (1 + Rate / n)^(n x Time) - Principal |
| Principal (P) | Initial amount invested or loaned |
| Rate (r) | Annual interest rate expressed as a decimal |
| n | Number of compounding periods per year |
| Time (t) | Time the money is invested or borrowed for, in years |
Visualizing Growth: Simple vs. Compound Interest
Simple interest grows linearly, calculated only on the initial principal, making the growth predictable over time. Compound interest, however, accumulates on both the principal and the previously earned interest, accelerating growth exponentially.
Visualizing this difference reveals how compound interest leads to significantly higher savings or investment returns in the long term. Graphs often show simple interest as a straight line, while compound interest curves upward, reflecting its accelerating nature.
Common Real-Life Applications
Simple and compound interest are essential concepts in finance that influence everyday financial decisions. Understanding their applications helps individuals optimize savings, loans, and investments effectively.
- Savings Accounts - Simple interest is often used for short-term savings, providing straightforward interest calculations.
- Mortgages - Compound interest impacts mortgage loans, accumulating interest on both principal and previous interest.
- Credit Cards - Compound interest frequently applies to credit card debt, increasing the total amount owed over time.
- Fixed Deposits - Simple interest is commonly used in fixed deposits, ensuring predictable returns.
- Investment Growth - Compound interest drives exponential growth in long-term investment portfolios.
Formulas at a Glance
Simple interest calculates earnings based on the principal amount over a set period using the formula I = P x r x t, where I is interest, P is principal, r is rate, and t is time. Compound interest considers interest on both principal and accrued interest, following the formula A = P(1 + r/n)^(nt), where A is the amount, n is compounding frequency. Understanding these formulas helps in comparing investment growth and loan costs effectively.
Pros and Cons of Each Interest Type
Simple and compound interest are fundamental concepts in finance that impact savings and loans. Understanding their advantages and drawbacks helps in making informed investment decisions.
- Simple Interest is easy to calculate - Its straightforward formula makes it accessible for quick financial assessments.
- Compound Interest grows wealth faster - Interest is earned on both the principal and accumulated interest, leading to exponential growth.
- Simple Interest limits earning potential - It does not account for interest on interest, resulting in slower growth over time.
- Compound Interest can be complex - Calculations require careful tracking of interest periods and compounding frequency.
- Simple Interest suits short-term loans - It is ideal when interest accrued over a short term is preferred to be linear.
Choosing between simple and compound interest depends on financial goals, loan terms, and investment horizons.
