Polynomial functions are fundamental mathematical expressions composed of variables and coefficients combined using addition, subtraction, and multiplication. Understanding their behavior through graphs helps illustrate key properties such as degree, roots, and end behavior. This infographic visually breaks down the essential components and characteristics of polynomial functions for clearer comprehension.
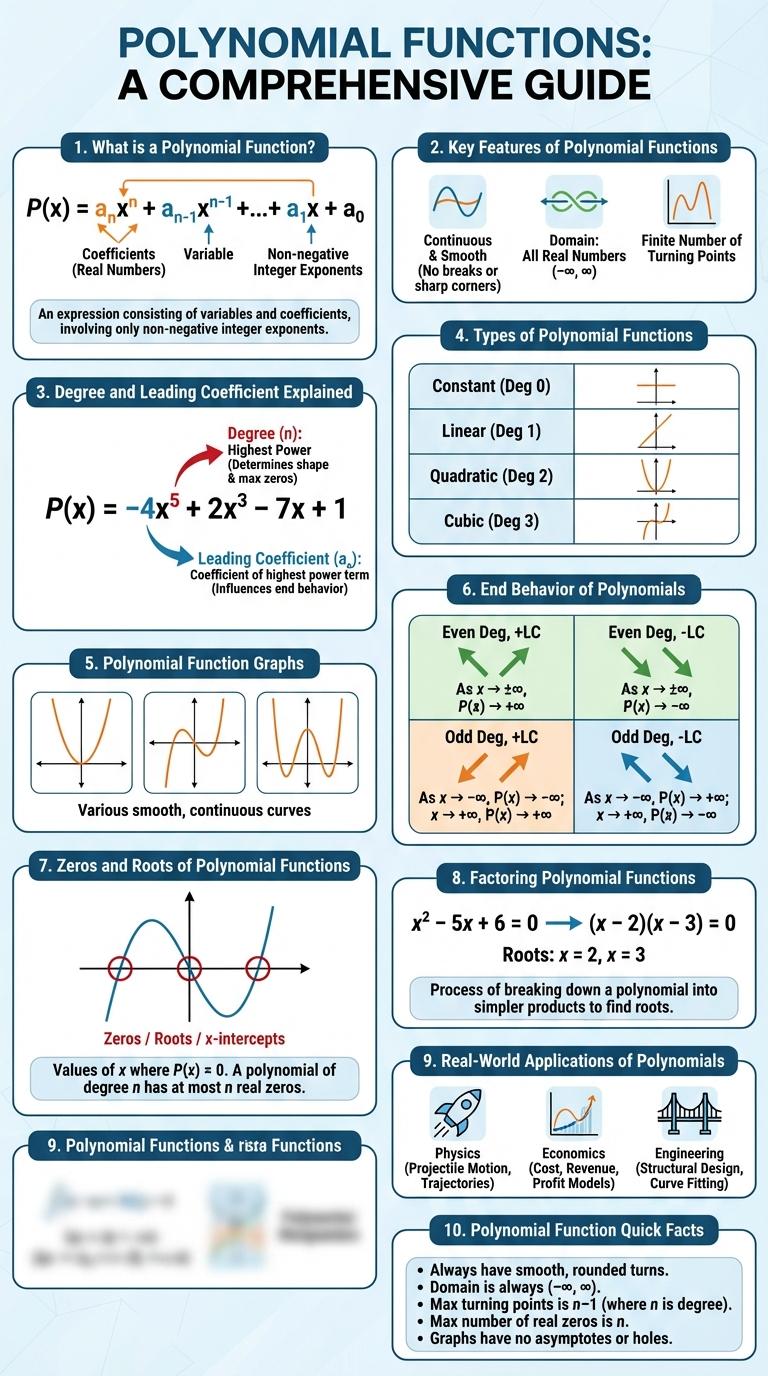
What is a Polynomial Function?
| Term | Description |
|---|---|
| Polynomial Function | A mathematical expression involving a sum of powers of a variable, multiplied by coefficients. |
| General Form | f(x) = a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0, where n is a non-negative integer. |
| Degree | The highest power of the variable in the polynomial, denoted by n in the general form. |
| Coefficients | Constants a_n, a_{n-1}, ..., a_0 that multiply each power of the variable, with a_n 0. |
| Variable | The symbol (commonly x) representing an unknown or changing value in the function. |
Key Features of Polynomial Functions
Polynomial functions are algebraic expressions consisting of variables raised to non-negative integer exponents combined using addition, subtraction, and multiplication. They are fundamental in mathematics due to their smooth and continuous curves that model various real-world phenomena.
- Degree of the Polynomial - Determines the highest power of the variable, influencing the shape and end behavior of the graph.
- Number of Roots - A polynomial of degree n has at most n real roots, including repeated roots.
- Continuity and Smoothness - Polynomial functions are continuous and differentiable everywhere on the real number line.
Degree and Leading Coefficient Explained
Polynomial functions are algebraic expressions consisting of variables raised to non-negative integer powers and coefficients. The degree and leading coefficient significantly influence the function's shape and behavior.
- Degree of a Polynomial - The degree is the highest power of the variable in the polynomial expression.
- Leading Coefficient - The leading coefficient is the coefficient of the term with the highest degree.
- Impact on Graph - The degree determines the number of roots and turning points, while the leading coefficient affects the end behavior of the graph.
Understanding the degree and leading coefficient helps predict polynomial graph characteristics efficiently.
Types of Polynomial Functions
What are the different types of polynomial functions? Polynomial functions are classified based on their degree and the number of terms they contain. Common types include monomials, binomials, trinomials, and higher-degree polynomials.
How do the degrees of polynomial functions determine their classification? The degree indicates the highest power of the variable in the function. For example, linear functions have degree 1, quadratic functions have degree 2, and cubic functions have degree 3.
| Type | Definition |
|---|---|
| Monomial | Polynomial with one term (e.g., 7x3) |
| Binomial | Polynomial with two terms (e.g., x2 + 5) |
| Trinomial | Polynomial with three terms (e.g., x2 - 3x + 2) |
| Linear | Degree 1 polynomial (e.g., 2x + 1) |
| Quadratic | Degree 2 polynomial (e.g., x2 - 4x + 4) |
Polynomial Function Graphs
Polynomial function graphs illustrate the behavior of polynomial equations by plotting their values on a coordinate plane. These graphs reveal key characteristics such as roots, turning points, and end behavior.
- Degree of the Polynomial - The degree determines the maximum number of turning points and influences the overall shape of the graph.
- Roots or Zeros - Points where the graph intersects the x-axis represent the solutions of the polynomial equation.
- End Behavior - The leading coefficient and degree dictate how the graph behaves as x approaches positive or negative infinity.
End Behavior of Polynomials
The end behavior of polynomial functions describes how the values of the function behave as the input approaches positive or negative infinity. It depends on the degree and leading coefficient of the polynomial.
For even-degree polynomials with a positive leading coefficient, both ends of the graph rise to positive infinity. If the leading coefficient is negative, the ends fall to negative infinity. Odd-degree polynomials have opposite ends: if the leading coefficient is positive, the graph falls on the left and rises on the right; if negative, it rises on the left and falls on the right.
Zeros and Roots of Polynomial Functions
Polynomial functions have zeros or roots where the function's value equals zero. These points indicate where the graph of the polynomial intersects the x-axis. Finding zeros involves solving the polynomial equation by factoring, using the quadratic formula, or applying numerical methods.
Factoring Polynomial Functions
Factoring polynomial functions involves expressing a polynomial as a product of its factors. This process simplifies solving equations and analyzing functions.
Common methods include factoring out the greatest common factor, grouping, and using special formulas like the difference of squares. Factoring helps reveal the roots and behavior of polynomial functions.
Real-World Applications of Polynomials
Polynomial functions play a crucial role in various real-world applications such as physics, engineering, and economics. They are used to model trajectories of objects, optimize resource allocation, and predict economic trends. Understanding polynomial behavior allows for accurate analysis and problem solving in these fields.
