Mathematics is a universal language that shapes the way we understand the world, from fundamental arithmetic to advanced calculus. Visual representations such as infographics simplify complex mathematical concepts, making them more accessible and engaging for learners of all levels. This infographic highlights key mathematical principles and their real-world applications, illustrating the beauty and practicality of math in everyday life.
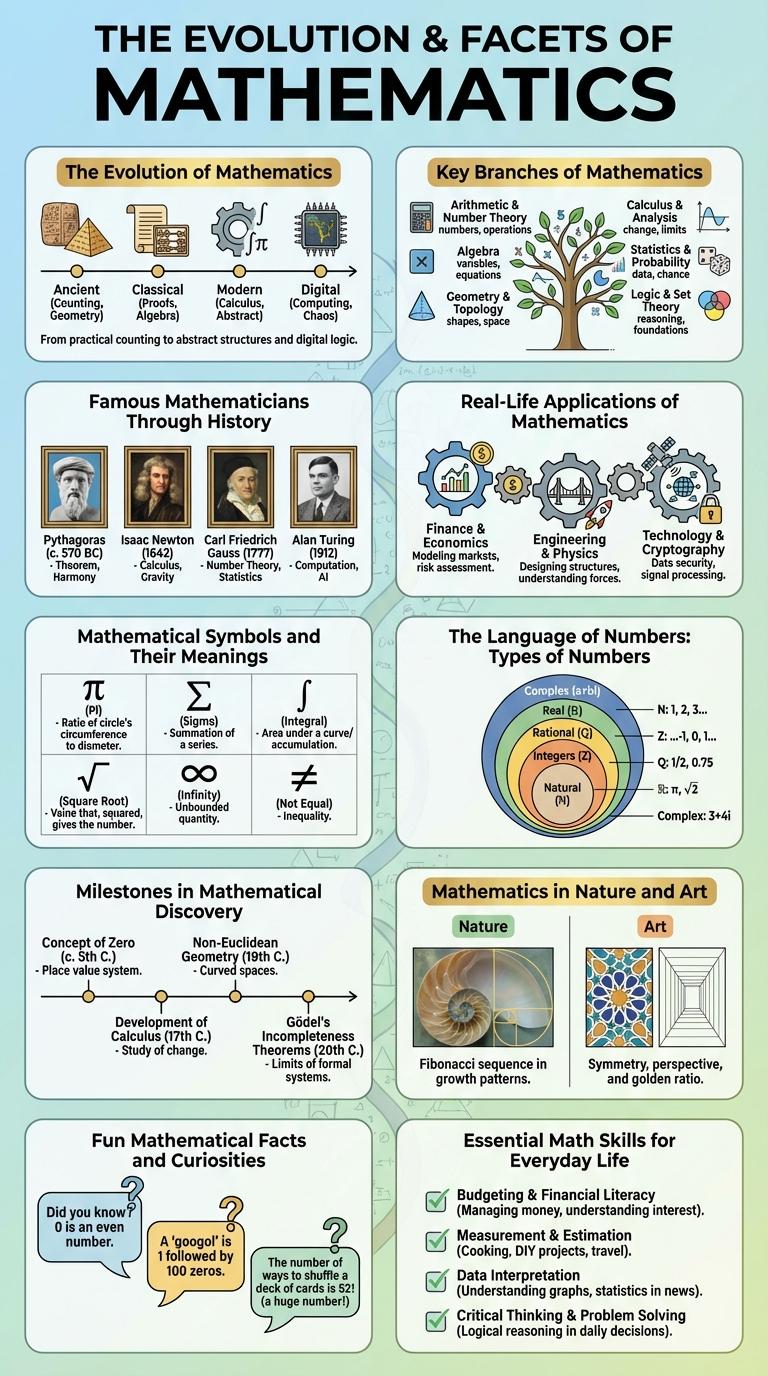
The Evolution of Mathematics
Mathematics has evolved over thousands of years, originating from basic counting and measurement systems in ancient civilizations such as Mesopotamia and Egypt. Early mathematicians developed concepts in arithmetic, geometry, and algebra that laid the foundation for modern mathematical theory.
During the Greek era, figures like Euclid and Pythagoras formalized principles of geometry and number theory. The Renaissance period saw a rapid expansion in mathematical knowledge, integrating calculus, probability, and abstract algebra, which propelled scientific and technological progress.
Key Branches of Mathematics
Mathematics consists of several key branches, each focusing on different concepts and applications. These branches include Algebra, Geometry, Calculus, Statistics, and Number Theory.
Algebra deals with symbols and rules for manipulating those symbols, while Geometry explores the properties and relations of points, lines, and shapes. Calculus studies change and motion, Statistics analyzes data and probability, and Number Theory investigates the properties of integers.
Famous Mathematicians Through History
Mathematics has been shaped by brilliant minds throughout history. Famous mathematicians like Euclid, Isaac Newton, Carl Gauss, Emmy Noether, and Alan Turing made groundbreaking contributions that advanced numerous fields. Their discoveries form the foundation of modern science, technology, and engineering.
Real-Life Applications of Mathematics
Mathematics plays a crucial role in solving real-world problems across various fields. Its principles help optimize systems, analyze data, and predict outcomes in everyday life.
- Finance Management - Mathematics helps individuals and businesses budget, invest, and assess financial risks effectively.
- Engineering Design - Mathematical calculations ensure structures are safe, functional, and efficient.
- Medical Imaging - Mathematics supports the development of technologies like MRI and CT scans for accurate diagnostics.
Mathematical Symbols and Their Meanings
Mathematical symbols are essential tools that represent numbers, operations, relations, and concepts in mathematics. They provide a universal language for expressing complex ideas clearly and efficiently.
Understanding these symbols enables better problem-solving and communication within all branches of mathematics.
- Plus (+) - Represents the operation of addition, combining two quantities into a larger one.
- Equals (=) - Indicates equality, showing that two expressions represent the same value.
- Pi (p) - Represents the ratio of a circle's circumference to its diameter, approximately 3.14159.
- Integral () - Symbolizes the integral in calculus, used to calculate areas under curves.
- Summation () - Denotes the sum of a sequence of numbers, typically used for series and sequences.
The Language of Numbers: Types of Numbers
Mathematics is a universal language composed of various types of numbers that help describe and solve problems. Understanding the different categories of numbers is fundamental to mastering mathematical concepts.
- Natural Numbers - These are the counting numbers starting from 1, used for basic enumeration.
- Whole Numbers - Natural numbers including zero, representing all non-negative integers.
- Integers - All positive and negative whole numbers, including zero, used to express values with direction.
- Rational Numbers - Numbers expressed as a fraction of two integers, where the denominator is not zero.
- Irrational Numbers - Numbers that cannot be expressed as fractions, having non-repeating, non-terminating decimal expansions.
Mastering these types of numbers enables clearer communication and deeper understanding of mathematical problems.
Milestones in Mathematical Discovery
What are the key milestones in the history of mathematical discovery? Mathematics has evolved through significant breakthroughs that shaped our understanding of the world. These milestones highlight the development of fundamental concepts and methods.
| Milestone | Impact |
|---|---|
| Ancient Geometry (circa 3000 BCE) | Foundation of shapes, measurement, and spatial relationships developed by Egyptians and Babylonians. |
| Euclid's Elements (circa 300 BCE) | Systematized geometry with axioms and theorems, forming the basis of classical mathematics. |
| Introduction of Zero (5th century CE) | Conceptualized in India, zero revolutionized arithmetic and number systems worldwide. |
| Calculus Development (17th century) | Isaac Newton and Gottfried Wilhelm Leibniz established calculus, enabling advances in physics and engineering. |
| Godel's Incompleteness Theorems (1931) | Proved limits of formal mathematical systems, influencing logic and computer science. |
Mathematics in Nature and Art
Mathematics reveals the hidden patterns and structures present in nature and art. From the spirals of shells to the proportions in classical paintings, math shapes the world around us.
In nature, the Fibonacci sequence appears in flower petals, pinecones, and hurricanes, illustrating growth and harmony. Fractals describe complex shapes like snowflakes and mountain ranges through repeating patterns at different scales. Artists use the golden ratio to create visually pleasing compositions, ensuring balance and aesthetic appeal.
Fun Mathematical Facts and Curiosities
| Mathematical Fact | Description |
|---|---|
| Zero is Unique | Zero is the only number that is neither negative nor positive, acting as the neutral element in arithmetic. |
| Pi is Infinite | The number p (pi) is an irrational number with an infinite, non-repeating decimal expansion starting with 3.14159. |
| Fibonacci Sequence in Nature | The Fibonacci sequence appears in nature, such as in the arrangement of leaves, flowers, and shells. |
| Prime Numbers | Prime numbers are numbers greater than 1 with no divisors other than 1 and themselves; they are the building blocks of integers. |
| Euler's Identity | Euler's identity, e^(ip) + 1 = 0, links five fundamental mathematical constants in a single elegant equation. |
