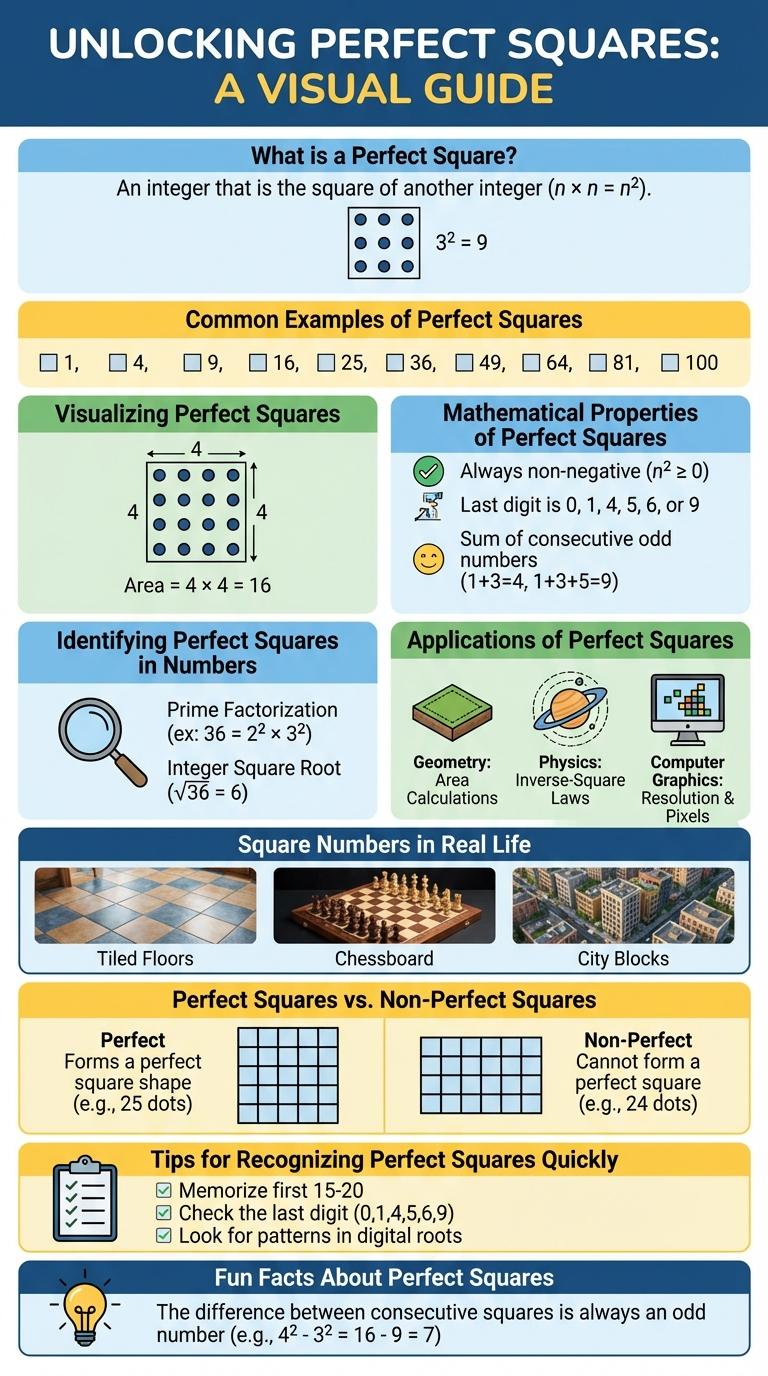
Perfect squares are numbers obtained by multiplying an integer by itself, forming a fundamental concept in mathematics. Visualizing perfect squares through an infographic enhances understanding of their properties and patterns. This graphic representation aids in grasping the relationship between square numbers and geometric shapes.
What is a Perfect Square?
A perfect square is a number that can be expressed as the product of an integer multiplied by itself. Examples include 1, 4, 9, 16, and 25, which are squares of 1, 2, 3, 4, and 5 respectively. Perfect squares have unique properties in mathematics, such as having an odd number of total divisors.
Common Examples of Perfect Squares
| Number | Perfect Square |
|---|---|
| 2 | 4 |
| 3 | 9 |
| 5 | 25 |
| 10 | 100 |
| 12 | 144 |
Visualizing Perfect Squares
Perfect squares are numbers generated by multiplying an integer by itself, such as 1, 4, 9, and 16. Visualizing perfect squares involves arranging objects or dots into equal square shapes, helping to understand their geometric significance. This infographic highlights key perfect squares and demonstrates their visual patterns for easy comprehension.
Mathematical Properties of Perfect Squares
Perfect squares are integers that can be expressed as the product of an integer with itself. They have unique mathematical properties that distinguish them from other numbers.
- Integral Square Roots - Every perfect square has an integer as its square root, ensuring precise root values without decimals.
- Odd Number Sum Representation - Each perfect square is the sum of a consecutive sequence of odd numbers starting from 1.
- Last Digit Patterns - Perfect squares in base 10 end only with digits 0, 1, 4, 5, 6, or 9, creating identifiable digit patterns.
Understanding these properties enables deeper insight into number theory and enhances problem-solving techniques.
Identifying Perfect Squares in Numbers
How can you identify perfect squares in numbers? Perfect squares are integers that can be expressed as the product of an integer multiplied by itself. Recognizing these numbers helps simplify problem-solving in math and enhances number sense.
| Number | Is it a Perfect Square? |
|---|---|
| 16 | Yes (4 x 4) |
| 20 | No |
| 49 | Yes (7 x 7) |
| 50 | No |
| 81 | Yes (9 x 9) |
Applications of Perfect Squares
Perfect squares play a crucial role in various fields, from mathematics to computer science. Their unique properties simplify complex calculations and problem-solving techniques.
In architecture, perfect squares help in designing precise layouts and structures. In coding theory, they optimize algorithms for error detection and correction.
Square Numbers in Real Life
Perfect squares are numbers that result from multiplying an integer by itself, such as 1, 4, 9, and 16. These square numbers frequently appear in various real-life scenarios, making them fundamental in mathematics and practical applications.
In architecture, square numbers help calculate areas, ensuring accurate measurements for floor plans and tiles. Square numbers are also used in computer science, particularly in algorithm optimization and memory allocation for efficient data storage.
Perfect Squares vs. Non-Perfect Squares
Perfect squares are integers that can be expressed as the square of an integer. Non-perfect squares cannot be written as the product of an integer multiplied by itself.
- Perfect Squares - Numbers like 1, 4, 9, and 16 have integer square roots.
- Non-Perfect Squares - Numbers such as 2, 3, 5, and 7 have non-integer square roots.
- Mathematical Properties - Perfect squares have an odd number of total factors, while non-perfect squares have an even number.
Tips for Recognizing Perfect Squares Quickly
Perfect squares are numbers that can be expressed as the product of an integer multiplied by itself. Recognizing them quickly helps in simplifying math problems and improving calculation speed.
Look for numbers ending in 0, 1, 4, 5, 6, or 9, as these are common last digits of perfect squares. Check the digital root: perfect squares have digital roots of 1, 4, 7, or 9. Memorizing squares of numbers 1 through 20 also speeds up identification.
