An infographic about function visually breaks down how inputs are transformed into outputs through specific rules or relationships. It highlights key concepts such as domain, range, and mapping in a clear, concise format to enhance understanding. This tool simplifies complex mathematical ideas, making them accessible to diverse audiences.
Understanding Functions: An Overview
What is a function in mathematics?
A function is a relation that uniquely associates elements of one set with elements of another set. Each input in the domain corresponds to exactly one output in the range.
How are functions represented?
Functions can be represented using tables, graphs, formulas, or mappings. Each method visually or numerically shows the relationship between input and output values.
Why are functions important in mathematics?
Functions model real-world phenomena and describe how one quantity depends on another. They form the foundation for calculus, physics, engineering, and computer science.
What are examples of common functions?
Linear, quadratic, polynomial, exponential, and trigonometric functions are common types. Each has distinct formulas and properties suitable for different applications.
How do you determine if a relation is a function?
Use the vertical line test on its graph to check if every vertical line intersects the graph at most once. This ensures each input has a unique output.
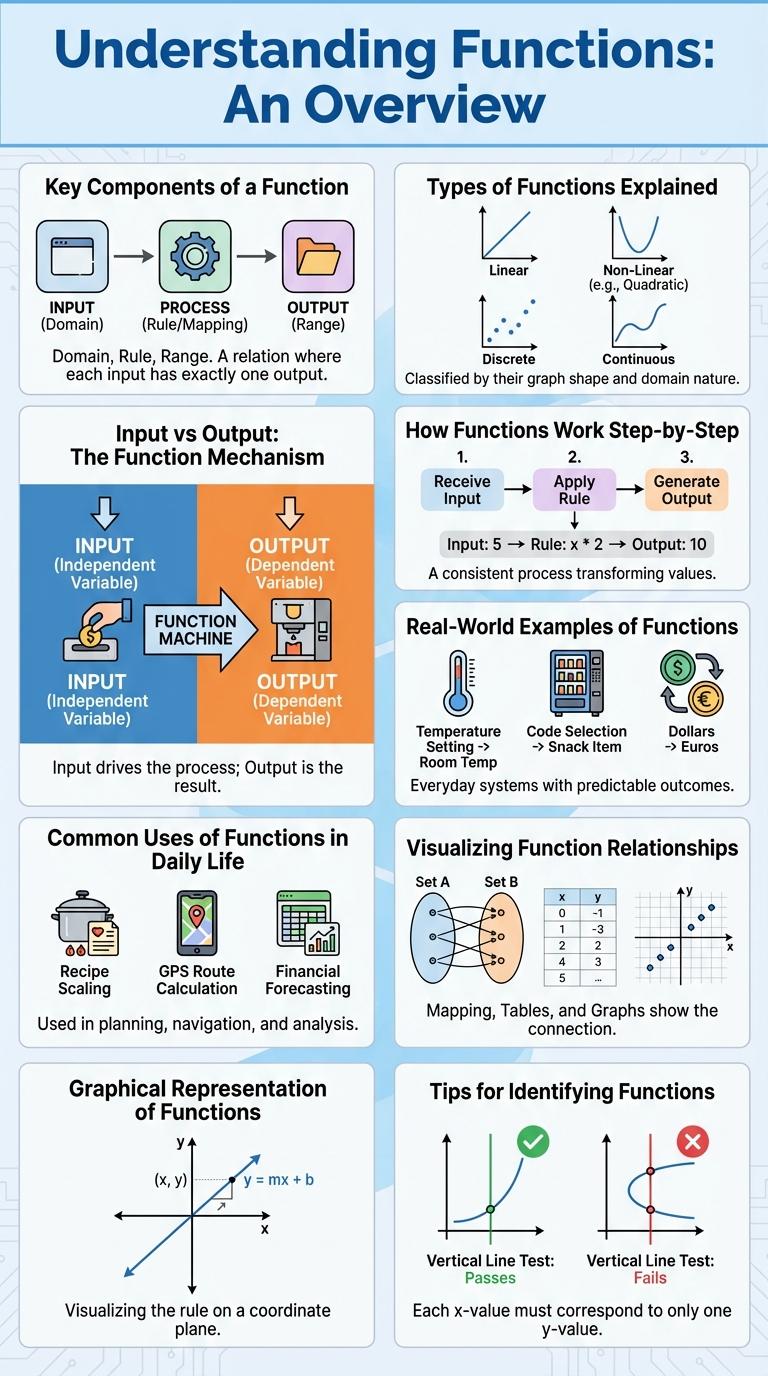
Key Components of a Function
Functions are fundamental building blocks in programming that enable code reuse and modular design. Understanding the key components of a function helps in writing clear and efficient code.
- Function Name - Identifies the function and is used to call it within a program.
- Parameters - Inputs passed to the function to customize its operation or behavior.
- Return Value - The output produced by the function after processing inputs.
Types of Functions Explained
Functions are mathematical relations where each input corresponds to exactly one output, forming the foundation of algebra and calculus. Types of functions include linear, quadratic, polynomial, exponential, and logarithmic, each with unique properties and applications. Understanding these function types helps solve equations, model real-world phenomena, and analyze data effectively.
How Functions Work Step-by-Step
Functions are reusable blocks of code designed to perform specific tasks. They help break down complex problems into manageable steps.
- Function Declaration - The function is defined with a name and optional parameters to specify inputs.
- Function Invocation - The function is called or invoked to execute its code with provided arguments.
- Return Statement - The function sends back a result or output after processing the input data.
Understanding how functions operate enables efficient and organized programming.
Input vs Output: The Function Mechanism
Functions are fundamental blocks in programming that take inputs, process them, and produce outputs. They encapsulate specific tasks, making code modular and reusable.
The input represents the data or arguments fed into the function, which undergoes a defined set of operations. The output is the result returned after the function executes its logic, reflecting transformations on the input.
Real-World Examples of Functions
Functions are fundamental concepts in mathematics and computer science used to map inputs to specific outputs. They model relationships and processes across various real-world scenarios.
- Temperature Conversion - A function converts Celsius to Fahrenheit by applying a precise mathematical formula.
- Bank Interest Calculation - Functions determine the amount of interest earned over time based on principal and rate.
- Inventory Management - Functions track stock levels by calculating additions and subtractions of products in real time.
Visualizing Function Relationships
| Concept | Description |
|---|---|
| Function Definition | A function describes a relationship where each input is linked to exactly one output. |
| Graphical Representation | Functions are visualized using graphs that plot inputs (x-values) on the horizontal axis and outputs (y-values) on the vertical axis. |
| Types of Functions | Common types include linear, quadratic, exponential, and trigonometric, each with distinct curve shapes showing input-output relationships. |
| Function Behavior | Visualization reveals key behaviors such as increasing/decreasing intervals, maxima and minima, continuity, and points of inflection. |
| Real-world Applications | Visualizing functions assists in understanding phenomena in physics, economics, biology, and engineering through their mathematical models. |
Common Uses of Functions in Daily Life
Functions play a vital role in organizing tasks and solving problems efficiently. They allow us to break down complex activities into manageable steps.
In daily life, functions are used in cooking recipes to ensure consistent results, in budgeting to track expenses, and in fitness routines to monitor progress. They help streamline repetitive actions and improve accuracy. Understanding functions enhances problem-solving skills both at work and home.
Graphical Representation of Functions
Functions map inputs to outputs, showing relationships between variables. Graphical representations use coordinate planes to visualize these relationships clearly. Common graphs include lines, curves, and points that depict function behavior and trends.
