Rational functions represent ratios of polynomial expressions where the denominator is not zero, playing a crucial role in algebra and calculus. Understanding their behavior involves analyzing asymptotes, intercepts, and discontinuities, which reveal key characteristics of the function's graph. This infographic visually breaks down the essential components and properties of rational functions for clearer comprehension.
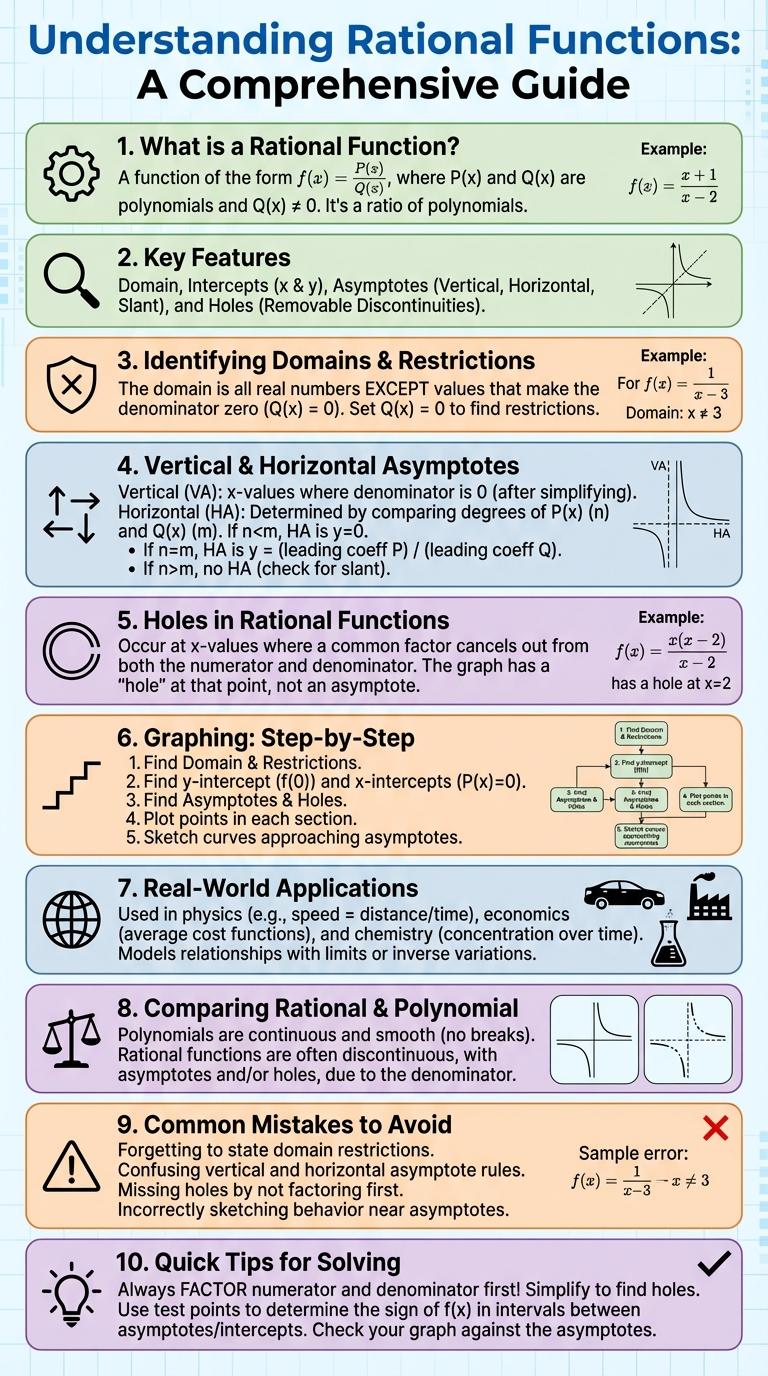
What is a Rational Function?
A rational function is a mathematical expression represented as the ratio of two polynomials, typically written as f(x) = P(x)/Q(x), where P(x) and Q(x) are polynomials and Q(x) 0. These functions can have vertical and horizontal asymptotes based on the zeros of the denominator and the degrees of the numerator and denominator polynomials. Rational functions are widely used in calculus, engineering, and physics to model relationships involving rates, proportions, and growth.
Key Features of Rational Functions
Rational functions are ratios of two polynomials and exhibit distinct characteristics useful in algebra and calculus. Understanding these features aids in graphing and analyzing their behavior effectively.
- Domain Restrictions - Values that make the denominator zero are excluded from the domain.
- Vertical Asymptotes - Occur where the denominator equals zero, indicating points of infinite discontinuity.
- Horizontal or Oblique Asymptotes - Describe end behavior determined by the degrees of the numerator and denominator polynomials.
Recognizing these key features is essential for solving, graphing, and applying rational functions in various mathematical contexts.
Identifying Domains and Restrictions
Rational functions are expressed as the ratio of two polynomials. Determining their domains requires identifying values that make the denominator zero.
To find domain restrictions, set the denominator equal to zero and solve for the variable. These values are excluded from the domain because they cause division by zero. Properly identifying these restrictions ensures accurate function analysis and graphing.
Vertical and Horizontal Asymptotes
A rational function is a ratio of two polynomials, often expressed as f(x) = P(x) / Q(x). Understanding its behavior involves analyzing vertical and horizontal asymptotes, which indicate values that the function approaches but never reaches.
Vertical asymptotes occur where the denominator Q(x) equals zero, causing the function to approach infinity or negative infinity. Horizontal asymptotes describe the end behavior of the function as x approaches positive or negative infinity, based on the degrees of the polynomials.
Holes in Rational Functions
Holes in rational functions occur when both the numerator and denominator share a common factor that cancels out. These points are removable discontinuities where the function is undefined but can be simplified.
Identifying holes helps in graphing rational functions accurately and understanding their behavior near undefined points.
- Common Factor - A hole exists where the numerator and denominator have a common factor that cancels out.
- Undefined Point - Holes represent points where the function is undefined due to zero in the denominator.
- Removable Discontinuity - After simplification, the hole is a removable discontinuity, indicating a missing point on the graph.
Graphing a Rational Function: Step-by-Step
| Step | Description |
|---|---|
| Identify Domain | Determine values of x that make the denominator zero. Exclude these from the domain. |
| Find Vertical Asymptotes | Set the denominator equal to zero and solve for x. These x-values are vertical asymptotes. |
| Find Horizontal or Oblique Asymptotes | Compare degrees of numerator and denominator:
|
| Calculate Intercepts |
|
| Plot Points and Sketch | Plot vertical & horizontal/oblique asymptotes, intercepts, and additional points. Sketch the curve respecting asymptotes and domain restrictions. |
Real-World Applications
How are rational functions used in real-world applications? Rational functions model relationships involving rates and ratios, such as speed, concentration, and economics. They help predict behavior in complex systems where variables influence each other proportionally.
| Application | Description |
|---|---|
| Engineering | Modeling system responses in control systems and signal processing. |
| Biology | Describing enzyme kinetics and population growth rates. |
| Economics | Analyzing cost functions, supply and demand curves. |
| Physics | Representing inverse relations such as intensity and distance. |
| Medicine | Modeling drug concentration and elimination rates in the body. |
Comparing Rational and Polynomial Functions
Rational functions are expressions formed by the ratio of two polynomials, while polynomial functions consist of sums of powers of variables with non-negative integer exponents. Rational functions often exhibit vertical and horizontal asymptotes, unlike polynomial functions, which have smooth continuous curves without asymptotes. Both function types are fundamental in calculus and algebra, but rational functions can model more complex behaviors due to their variable denominators.
Common Mistakes to Avoid
Understanding rational functions is essential for mastering algebraic concepts. These functions involve ratios of polynomials and require careful manipulation to avoid errors.
Common mistakes include ignoring domain restrictions caused by zero denominators. Overlooking these restrictions leads to incorrect solutions and undefined values.
