Number systems organize and represent numerical values using specific symbols and rules. Common types include decimal, binary, octal, and hexadecimal systems, each serving unique purposes in mathematics and computing. Understanding these systems enhances data interpretation and facilitates efficient digital communication.
Introduction to Number Systems
Number systems are fundamental frameworks used to represent and express numbers in various forms. They provide the basis for mathematical operations, computing, and everyday counting.
Common number systems include decimal, binary, octal, and hexadecimal, each with unique symbols and positional values. Understanding these systems is essential for fields such as computer science and digital electronics.
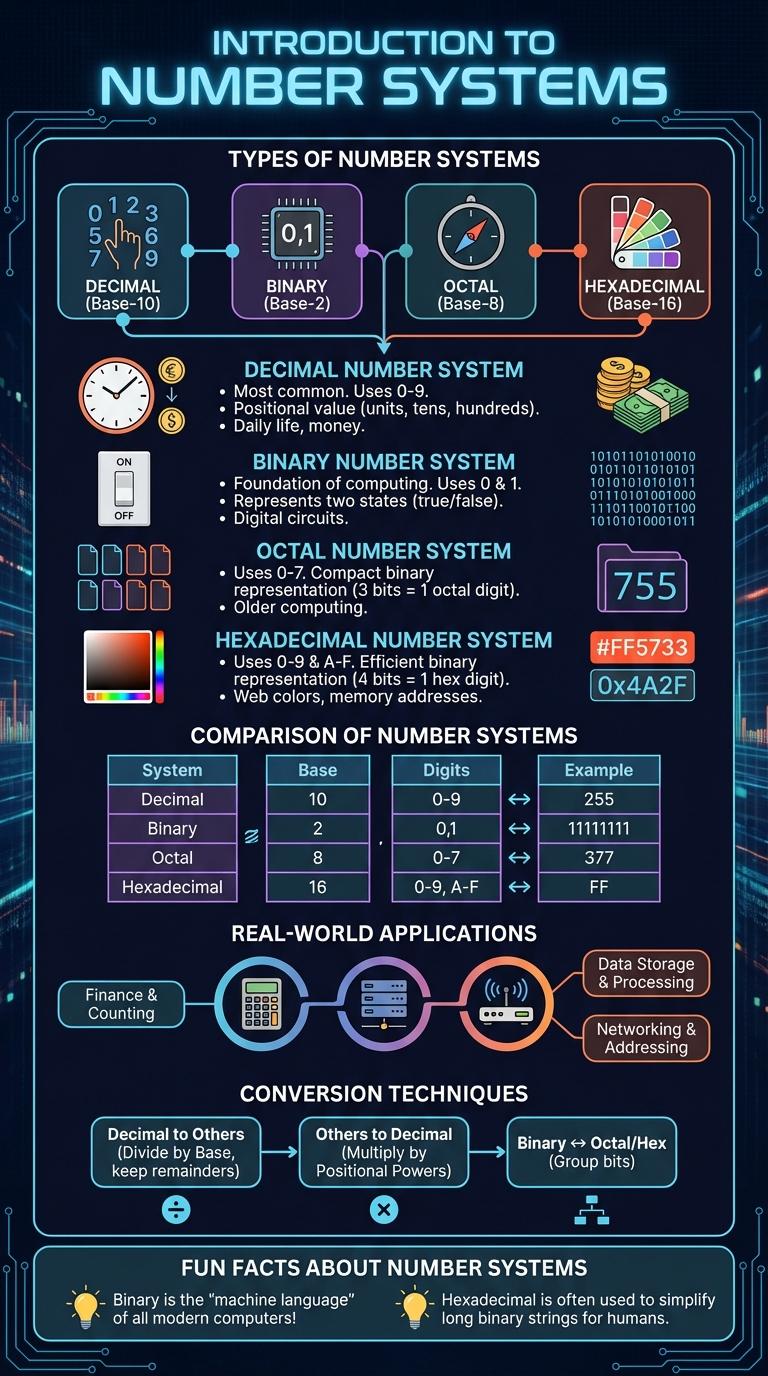
Types of Number Systems
Number systems form the foundation of mathematics and computing, representing values using distinct symbols and rules. Various types of number systems exist, each suited for different applications and levels of complexity.
- Decimal System - Uses base 10 with digits from 0 to 9 and is the most widely used system for daily counting and arithmetic.
- Binary System - Employs base 2, using only 0 and 1, essential for digital electronics and computer operations.
- Hexadecimal System - A base 16 system that includes digits 0-9 and letters A-F, commonly used in programming and memory addressing.
Decimal Number System
The Decimal Number System is the most widely used number system in the world, based on ten digits from 0 to 9. It is also known as the base-10 system, reflecting its ten unique symbols.
Each digit's position represents a power of ten, starting from the right with 10^0. This system simplifies counting, arithmetic, and number representation in everyday life.
Binary Number System
The binary number system is the foundation of modern digital computing. It uses only two digits, 0 and 1, to represent all values.
- Base-2 System - Binary is a base-2 numeral system, unlike decimal which is base-10.
- Representation of Data - Computers use binary to encode all types of data, including numbers, text, and instructions.
- Bit and Byte - A single binary digit is called a bit; eight bits make a byte, the standard data unit in computing.
Binary arithmetic enables efficient and reliable computation in digital circuits.
Octal Number System
What is the Octal Number System? The octal number system is a base-8 numeral system that uses digits from 0 to 7. It is commonly used in computer science because it offers a more compact representation of binary numbers.
| Feature | Description |
|---|---|
| Base | 8 |
| Digits | 0 to 7 |
| Relation to Binary | Each octal digit represents 3 binary digits (bits) |
| Use | Compact representation of large binary numbers |
| Example | Octal 17 is binary 001 111, or decimal 15 |
Hexadecimal Number System
The hexadecimal number system is a base-16 numeral system widely used in computing and digital electronics. It uses sixteen distinct symbols: 0-9 to represent values zero to nine and A-F to represent values ten to fifteen. Hexadecimal simplifies binary code by grouping every four binary digits into one hex digit, making it easier to read and interpret large binary numbers.
Comparison of Number Systems
| Number System | Base & Symbols |
|---|---|
| Decimal | Base 10, Symbols: 0-9 |
| Binary | Base 2, Symbols: 0, 1 |
| Octal | Base 8, Symbols: 0-7 |
| Hexadecimal | Base 16, Symbols: 0-9, A-F |
| Roman | Non-positional, Symbols: I, V, X, L, C, D, M |
Real-World Applications
The number system forms the foundation of various real-world technologies and everyday applications. Understanding different types of number systems enables advancements in computing, engineering, and digital communications.
Real-world applications of number systems demonstrate their critical role in modern technology and practical uses across many industries.
- Computer Systems - Binary number system is the core language of computers, representing data and instructions efficiently.
- Digital Electronics - Hexadecimal and octal systems simplify the representation and debugging of binary-coded digital circuits.
- Financial Calculations - Decimal system is essential in accounting, banking, and currency transactions for accurate data handling.
Conversion Techniques
The number system consists of various bases such as binary, decimal, octal, and hexadecimal. Each system uses unique digits and place values to represent numbers efficiently.
Conversion techniques allow the transformation of numbers from one base to another accurately. Common methods include division-remainder for decimal to other bases and repeated multiplication for fractional parts. Understanding these techniques is essential for applications in computing and digital electronics.
