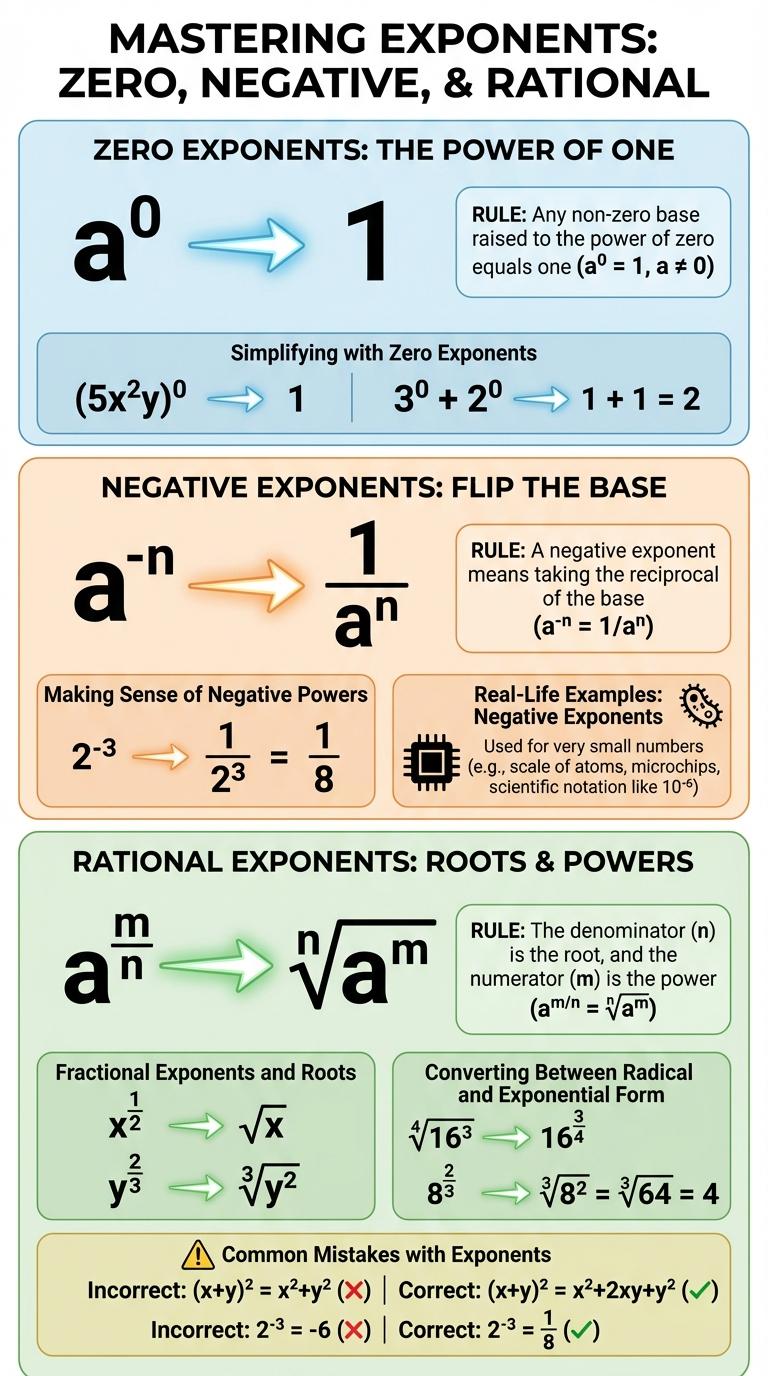
Zero, negative, and rational exponents represent key concepts that simplify expressions and solve equations efficiently. Understanding zero exponents reveals that any nonzero base raised to zero equals one, while negative exponents indicate the reciprocal of the base raised to the corresponding positive exponent. Rational exponents provide a way to represent roots and powers simultaneously, expanding the ability to work with fractional powers in algebra and calculus.
Understanding Zero Exponents
Zero exponents indicate that any nonzero base raised to the power of zero equals one. This rule applies universally across rational and integer bases, simplifying expressions efficiently. Understanding zero exponents is essential for mastering exponent rules and algebraic manipulations.
Negative Exponents Explained
Negative exponents represent the reciprocal of a base raised to a positive exponent. Understanding negative exponents helps simplify expressions and solve equations efficiently.
Rational exponents express roots and powers simultaneously, creating a bridge between radical and exponential forms.
- Negative Exponents Indicate Reciprocals - A base with a negative exponent is equivalent to one divided by the base with the corresponding positive exponent.
- Zero Exponent Equals One - Any non-zero base raised to the zero power is equal to one.
- Rational Exponents Represent Roots - An exponent expressed as a fraction, such as 1/n, corresponds to the nth root of the base.
What Are Rational Exponents?
What Are Rational Exponents? Rational exponents express roots and powers in a fractional form, combining both operations into a single notation. For example, a rational exponent like \(a^{m/n}\) represents the nth root of \(a\) raised to the mth power.
Zero Exponent Rule: The Power of One
The zero exponent rule states any nonzero number raised to the power of zero equals one. This fundamental rule simplifies expressions and ensures consistency in exponentiation.
For example, \(a^0 = 1\) where \(a \neq 0\). This applies to all real numbers and variables, reinforcing the concept of the power of one. The zero exponent rule is essential in algebra and higher mathematics for simplifying terms.
Making Sense of Negative Powers
| Concept | Description |
|---|---|
| Zero Exponent | Any non-zero number raised to the power of zero equals 1. Example: 50 = 1 |
| Negative Exponent | A negative exponent represents the reciprocal of the base raised to the positive exponent. Example: 4-2 = 1 / 42 = 1/16 |
| Rational Exponent | Rational exponents express roots and powers together. Example: 82/3 = (3rd root of 8)2 = 22 = 4 |
| Making Sense of Negative Powers | Negative powers invert the base. For example, x-n equals 1 / xn. This relationship helps simplify expressions and solve equations involving exponents. |
| Key Property | xa x xb = xa+b applies for zero, negative, and rational exponents, maintaining consistency in exponent rules. |
Fractional Exponents and Roots
Fractional exponents represent roots and powers simultaneously, offering a compact way to express expressions involving radicals. Understanding how to manipulate zero, negative, and rational exponents is essential for simplifying complex algebraic problems.
- Fractional Exponents and Roots - A fractional exponent like \(a^{\frac{m}{n}}\) means the nth root of \(a\) raised to the mth power.
- Zero Exponent Rule - Any nonzero number raised to the zero power equals 1, symbolizing the base's neutral element in multiplication.
- Negative Exponents - A negative exponent indicates the reciprocal of the base raised to the corresponding positive exponent, such as \(a^{-m} = \frac{1}{a^{m}}\).
Simplifying with Zero Exponents
Simplifying expressions with zero exponents follows a fundamental rule: any nonzero base raised to the zero power equals one. This principle is crucial for understanding and manipulating algebraic expressions efficiently.
For example, \(a^0 = 1\) where \(a \neq 0\). This applies universally to variables, numbers, and even complex expressions, streamlining calculations and simplifying results.
Real-Life Examples: Negative Exponents
Negative exponents represent the reciprocal of a number raised to a positive exponent, such as 2^-3 = 1/2^3 = 1/8. They appear in various real-life applications where values decrease or invert, demonstrating inverse relationships.
In scientific contexts, negative exponents are used to express very small quantities, like the size of atoms measured in nanometers (10^-9 meters). Financial calculations often apply negative exponents to model depreciation or discount rates over time.
Converting Between Radical and Exponential Form
Understanding zero, negative, and rational exponents is essential for mastering algebraic expressions. Converting between radical and exponential forms simplifies complex calculations and enhances problem-solving skills.
- Zero Exponent Rule - Any nonzero base raised to the zero power equals one, such as a0 = 1.
- Negative Exponents - A negative exponent indicates the reciprocal of the base raised to the corresponding positive exponent, like a-n = 1/an.
- Rational Exponents to Radicals - Rational exponents express roots, for example, am/n = √n(am).
Mastering these conversions empowers efficient manipulation of exponential and radical expressions in algebra.
