Parallel lines cut by a transversal create multiple angles with specific relationships, including corresponding, alternate interior, and alternate exterior angles. Understanding these angle pairs helps solve geometry problems involving parallel lines and transversals. Visualizing these concepts through an infographic enhances comprehension and retention.
Understanding Parallel Lines and Transversals
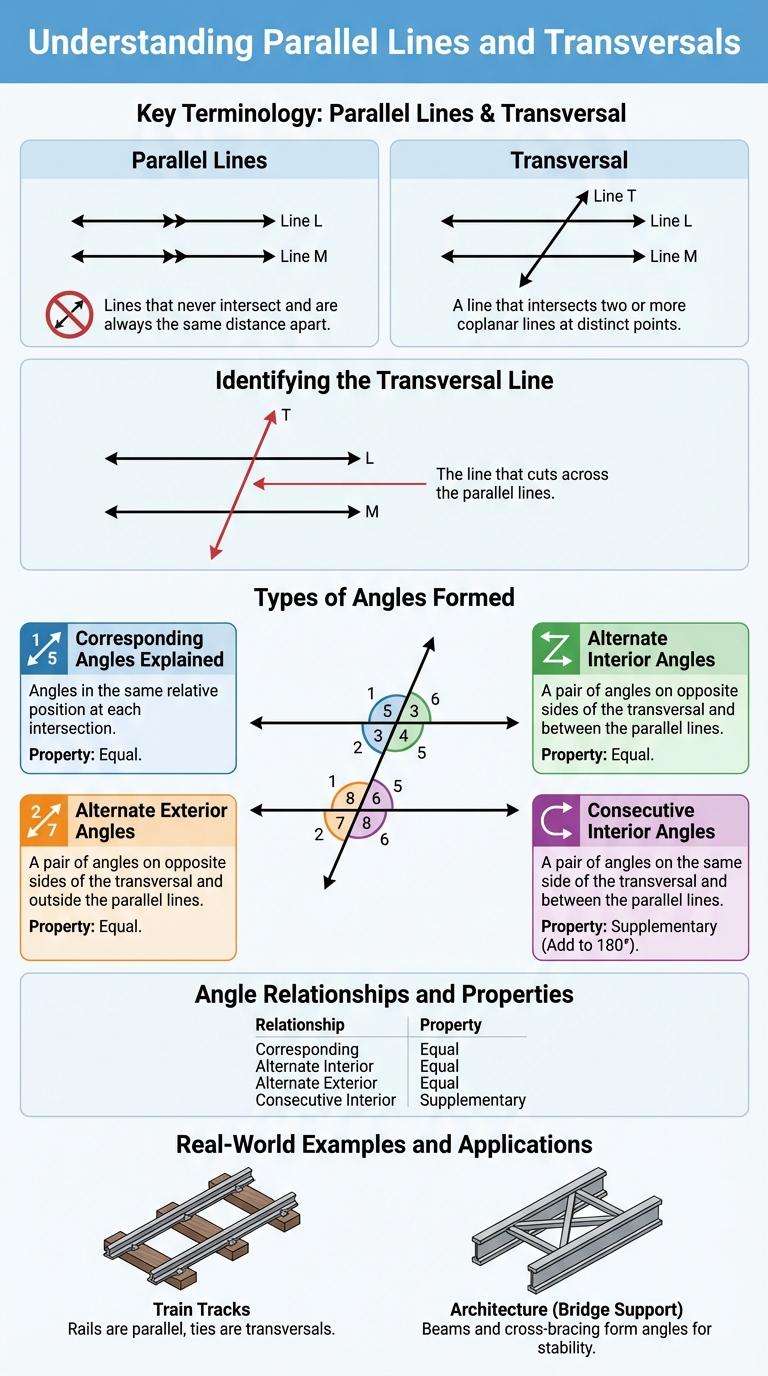
Parallel lines are two lines in a plane that never intersect, no matter how far they extend. A transversal is a line that crosses two or more parallel lines at distinct points.
When a transversal intersects parallel lines, it creates several angles that have special relationships. These angles include corresponding angles, alternate interior angles, and alternate exterior angles. Understanding these angle relationships helps in solving geometric problems and proving theorems.
Key Terminology: Parallel Lines & Transversal
Parallel lines are two lines in a plane that never meet, no matter how far they are extended. A transversal is a line that intersects two or more parallel lines at different points.
When a transversal crosses parallel lines, it creates several angle pairs with special properties. These angle relationships help solve many geometric problems related to parallel lines.
Identifying the Transversal Line
In geometry, a transversal line is a line that intersects two or more other lines at distinct points. When the lines being crossed are parallel, the transversal creates several pairs of angles with special relationships. Identifying the transversal is crucial for understanding angle properties such as alternate interior, corresponding, and consecutive interior angles.
Types of Angles Formed
When parallel lines are cut by a transversal, several types of angles are formed that have unique relationships. Understanding these angles helps in solving geometric problems involving parallel lines.
- Corresponding Angles - Angles in the same position on each parallel line and are equal.
- Alternate Interior Angles - Angles on opposite sides of the transversal and inside the parallel lines; they are congruent.
- Consecutive Interior Angles - Angles on the same side of the transversal and inside the parallel lines; their measures add up to 180 degrees.
Corresponding Angles Explained
What are corresponding angles when parallel lines are cut by a transversal? Corresponding angles are pairs of angles located in the same relative position at each intersection where a transversal crosses parallel lines. These angles are always equal in measure, making them useful for solving geometric problems.
Alternate Interior Angles
Parallel lines cut by a transversal create several angle pairs with unique properties. Alternate interior angles are pairs of angles located between the two lines and on opposite sides of the transversal.
- Definition - Alternate interior angles lie between the parallel lines and opposite sides of the transversal.
- Congruence - Alternate interior angles are always equal in measure when lines are parallel.
- Application - Identifying alternate interior angles helps determine if two lines are parallel in geometric proofs.
Alternate Exterior Angles
Parallel lines cut by a transversal create several angle pairs with unique relationships. Alternate exterior angles lie outside the parallel lines and on opposite sides of the transversal.
These angles are congruent, meaning they have equal measures. Recognizing alternate exterior angles helps solve geometry problems involving parallel lines and transversals.
Consecutive Interior Angles
Consecutive interior angles are pairs of angles located on the same side of the transversal and between the two parallel lines. These angles are supplementary, meaning their measures add up to 180 degrees. Identifying consecutive interior angles helps solve problems involving parallel lines and transversals in geometry.
Angle Relationships and Properties
Parallel lines cut by a transversal create various angle relationships that are fundamental in geometry. Understanding these angles helps in solving problems involving parallel lines and transversals.
- Corresponding Angles - Angles in the same position on parallel lines and the transversal are equal in measure.
- Alternate Interior Angles - Angles on opposite sides of the transversal, inside the parallel lines, are congruent.
- Consecutive Interior Angles - Also called same-side interior angles, their measures add up to 180 degrees.
These angle properties are essential for proving lines are parallel and for solving geometric equations involving transversals.
