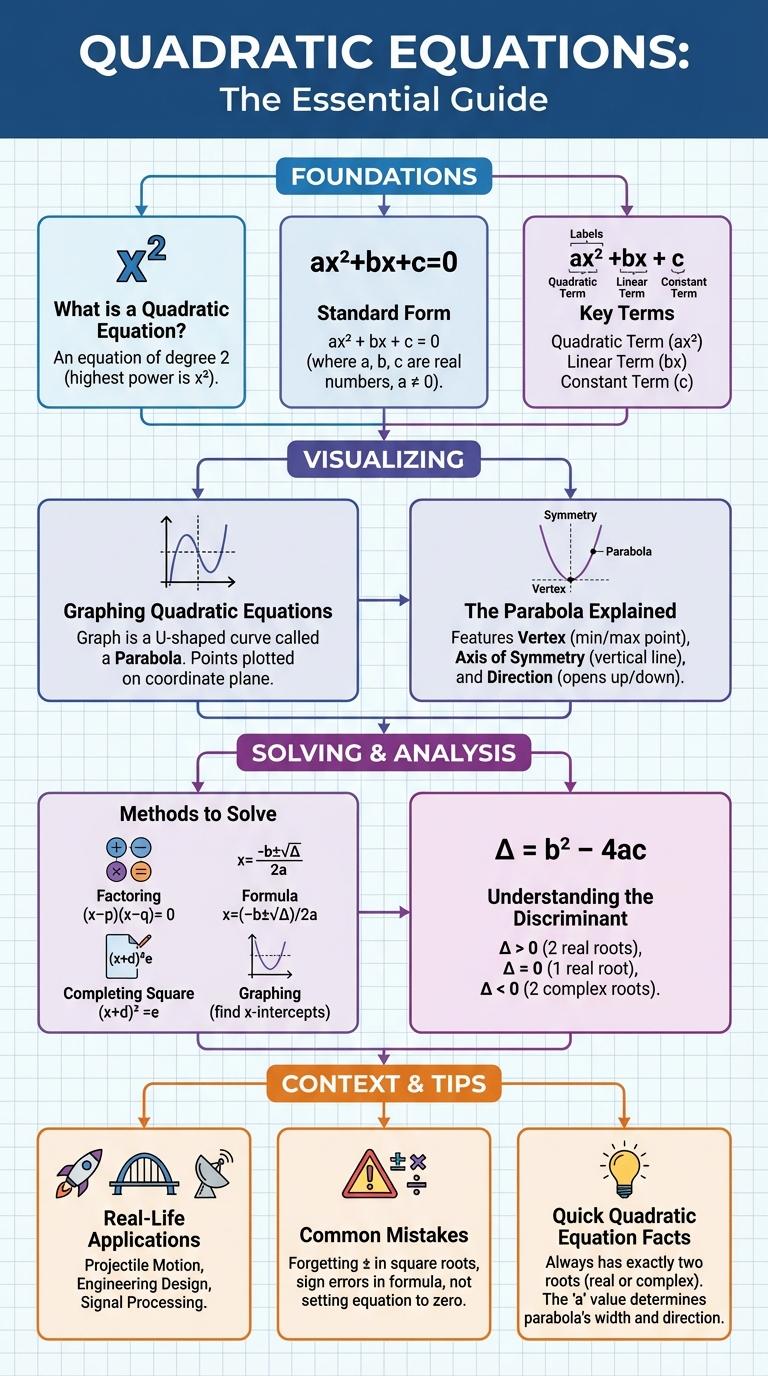
A quadratic equation is a fundamental concept in algebra characterized by the standard form ax2 + bx + c = 0, where a, b, and c are constants. Understanding its components and solutions, such as the vertex, axis of symmetry, and roots, is crucial for solving various mathematical problems. This infographic visually breaks down these elements, making the quadratic equation easier to grasp and apply effectively.
What is a Quadratic Equation?
What is a quadratic equation? A quadratic equation is a polynomial equation of degree two, typically written as ax2 + bx + c = 0. It describes a parabola when graphed on the coordinate plane.
Standard Form of Quadratic Equation
The standard form of a quadratic equation is expressed as ax2 + bx + c = 0, where a, b, and c are constants and a 0. This form is essential for analyzing the properties of a quadratic function.
Values of a, b, and c determine the shape and position of the parabola on the coordinate plane. The quadratic formula, vertex, and axis of symmetry all derive from this standard form.
Key Terms in Quadratics
The quadratic equation is a fundamental concept in algebra, representing equations of the form ax2 + bx + c = 0. Key terms in quadratics include coefficients, variables, and constants that define the equation's structure.
The term "discriminant" determines the nature of the roots, while "roots" or "solutions" are the values of the variable that satisfy the equation. Understanding these terms is essential for solving quadratic equations effectively.
Graphing Quadratic Equations
Graphing quadratic equations reveals the characteristic parabolic shape of their solutions. Understanding key features such as the vertex, axis of symmetry, and roots enhances the interpretation of quadratic graphs.
- Vertex Identification - The vertex represents the maximum or minimum point of the parabola and is calculated using the formula (-b/2a, f(-b/2a)).
- Axis of Symmetry - The axis of symmetry is a vertical line that passes through the vertex and divides the parabola into two mirror-image halves.
- Roots or Zeros - The roots are the x-values where the quadratic equation equals zero, indicating where the graph intersects the x-axis.
The Parabola Explained
The quadratic equation \( y = ax^2 + bx + c \) represents a parabola, a symmetrical curved graph. The coefficient \( a \) determines the parabola's direction and width, with positive values opening upwards and negative values downwards. The vertex, found at \( x = -\frac{b}{2a} \), is the parabola's highest or lowest point, indicating its maximum or minimum value.
Methods to Solve Quadratic Equations
Quadratic equations can be solved using various methods such as factoring, completing the square, and the quadratic formula. Each method provides a systematic approach to find the roots of the equation ax2 + bx + c = 0. Choosing the appropriate method depends on the specific coefficients and complexity of the quadratic expression.
| Method | Description |
|---|---|
| Factoring | Expresses the quadratic as a product of binomials to find roots directly. |
| Completing the Square | Transforms the equation into a perfect square trinomial for solving. |
| Quadratic Formula | Applies the formula x = [-b +- (b2-4ac)] / 2a to compute roots. |
| Graphing | Visualizes the parabola to locate x-intercepts that represent solutions. |
| Square Root Method | Used when the quadratic is in the form (x - p)2 = q to solve by taking square roots. |
Understanding the Discriminant
The discriminant in a quadratic equation reveals the nature of its roots. It is derived from the coefficients of the equation in the form ax2 + bx + c = 0.
- Discriminant Formula - Calculated as D = b2 - 4ac, it determines the type of solutions.
- Positive Discriminant - Indicates two distinct real roots for the quadratic equation.
- Zero Discriminant - Shows one real repeated root, meaning the parabola touches the x-axis once.
- Negative Discriminant - Implies no real roots, with solutions being complex or imaginary numbers.
- Graphical Interpretation - The discriminant value affects how the parabola intersects the x-axis on a coordinate plane.
Understanding the discriminant is essential for solving quadratic equations and predicting root behavior efficiently.
Real-Life Applications
| Application | Description |
|---|---|
| Projectile Motion | Quadratic equations model the trajectory of objects in sports, engineering, and physics to predict positions and optimize paths. |
| Architecture | Design of parabolic arches and bridges uses quadratic functions for structural integrity and aesthetic appeal. |
| Finance | Quadratic equations help calculate profit maximization and risk assessment in investment planning. |
| Biology | Modeling population growth and rates of change relies on quadratic functions to analyze trends over time. |
| Optics | Designing lenses and mirrors uses quadratic principles to focus light accurately. |
Common Mistakes in Quadratics
Quadratic equations often confuse students, leading to common errors that affect their solutions. Understanding these mistakes improves accuracy and confidence in solving quadratics.
Misidentifying the coefficient of the quadratic term can cause incorrect factoring or application of the quadratic formula. Forgetting to set the equation to zero before solving disrupts the solution process. Incorrect calculation of the discriminant leads to misunderstanding the nature of the roots.
