Moment of inertia measures an object's resistance to rotational motion around an axis, depending on the mass distribution relative to that axis. It plays a crucial role in engineering and physics, influencing the stability and dynamic behavior of rotating bodies. Understanding this concept aids in designing efficient machinery and structures by optimizing weight distribution for desired rotational performance.
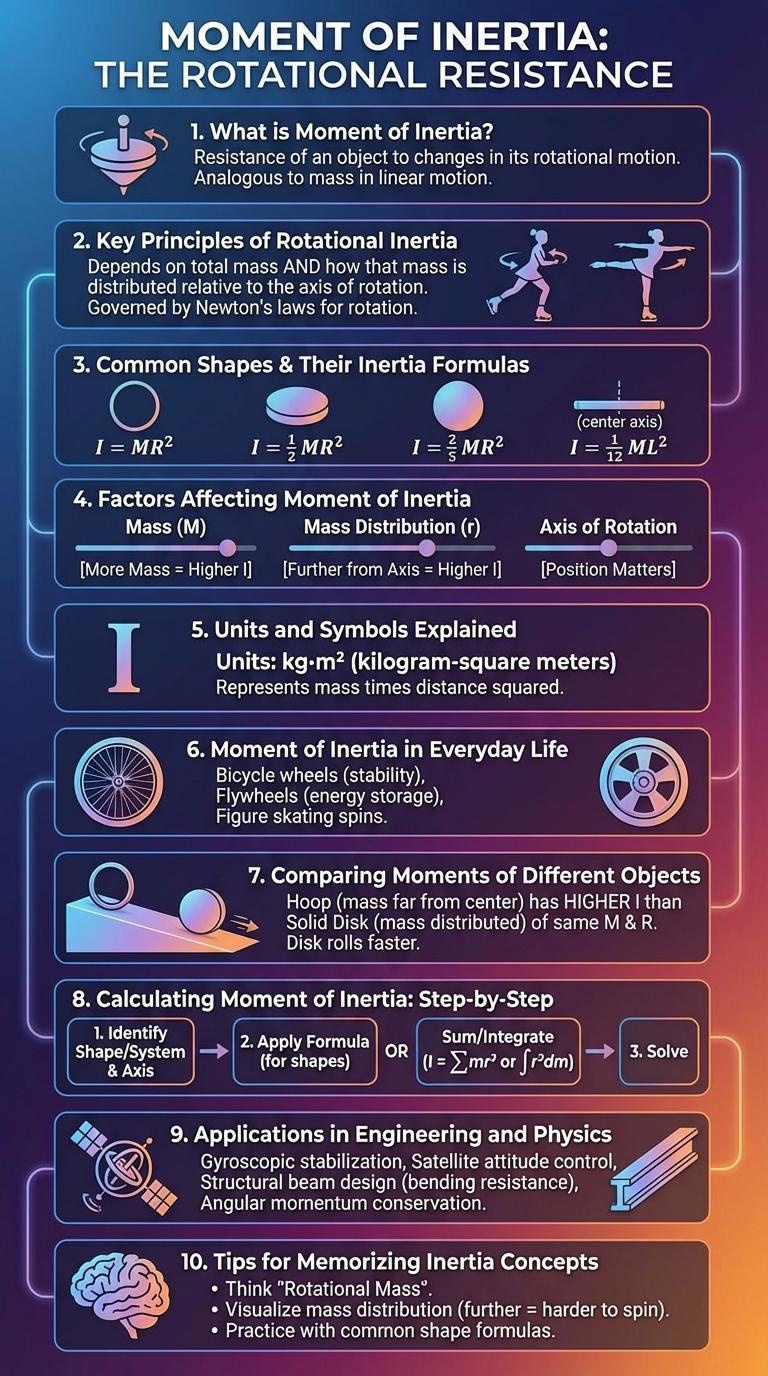
What is Moment of Inertia?
The moment of inertia is a physical quantity that measures an object's resistance to rotational motion around an axis. It depends on the object's mass distribution relative to the axis of rotation.
The moment of inertia plays a critical role in rotational dynamics, influencing how much torque is required to change an object's angular velocity. It varies with both the shape of the object and the location of the rotation axis. Engineers and physicists use this concept extensively when designing mechanical systems and analyzing rotational behavior.
Key Principles of Rotational Inertia
Moment of inertia quantifies an object's resistance to rotational acceleration about an axis. It depends on the mass distribution relative to the rotation axis.
- Mass Distribution - Moment of inertia increases as mass is positioned farther from the axis of rotation.
- Axis of Rotation - Different axes for the same object yield different moments of inertia due to varying mass arrangement.
- Shape Dependency - Geometrical shape influences how mass is distributed, directly affecting rotational inertia values.
Common Shapes and Their Inertia Formulas
The moment of inertia quantifies an object's resistance to rotational motion about an axis. It depends on the object's mass distribution relative to the axis of rotation.
Common geometric shapes have specific formulas to calculate their moments of inertia, useful in engineering and physics applications. These formulas consider shape, size, and axis orientation for accurate calculations.
| Shape | Moment of Inertia Formula |
|---|---|
| Solid Rectangle (about base) | (1/3) x mass x height2 |
| Solid Circle (about center) | (1/2) x mass x radius2 |
| Thin Rod (about center) | (1/12) x mass x length2 |
| Hollow Cylinder (about center) | mass x radius2 |
| Solid Sphere (about center) | (2/5) x mass x radius2 |
Factors Affecting Moment of Inertia
Moment of inertia measures an object's resistance to rotational motion around an axis. It depends on how mass is distributed relative to the axis of rotation.
- Mass - Greater mass increases the moment of inertia, making the object harder to rotate.
- Distance from Axis - Mass located farther from the axis significantly raises the moment of inertia.
- Shape and Geometry - Different shapes and mass distributions affect how the moment of inertia is calculated and its value.
Units and Symbols Explained
Moment of inertia is a measure of an object's resistance to rotational motion around an axis. It depends on the mass distribution relative to the axis of rotation.
The standard unit for moment of inertia in the International System of Units (SI) is kilogram meter squared (kg*m2). The symbol commonly used to represent moment of inertia is "I".
Moment of Inertia in Everyday Life
How does the moment of inertia affect the motion of everyday objects? Moment of inertia determines how much torque is needed for an object to achieve angular acceleration. This property influences the design of tools, vehicles, and sports equipment for optimal performance.
Comparing Moments of Different Objects
Moment of inertia quantifies an object's resistance to rotational motion, depending on mass distribution relative to the axis of rotation. Different shapes like solid spheres, hollow cylinders, and rods exhibit unique moments of inertia influenced by their geometry and mass allocation. Comparing these moments helps in understanding rotational dynamics and optimizing design in engineering applications.
| Object | Moment of Inertia Formula |
|---|---|
| Solid Sphere | (2/5)*m*r2 |
| Hollow Cylinder | m*r2 |
| Solid Rod (about center) | (1/12)*m*L2 |
| Thin Rectangular Plate | (1/12)*m*(a2 + b2) |
Calculating Moment of Inertia: Step-by-Step
Moment of inertia measures an object's resistance to rotational motion around a specific axis. Calculating it involves summing the products of mass elements and the square of their distances from the axis. This step-by-step process requires identifying the shape, determining mass distribution, and applying integral or formula-based methods.
Applications in Engineering and Physics
The moment of inertia is a fundamental property that quantifies an object's resistance to angular acceleration. It plays a crucial role in both engineering design and physical system analysis.
- Structural Engineering - Moment of inertia determines the bending resistance of beams and structural elements under load.
- Mechanical Systems - It is essential for calculating torque and angular momentum in rotating machinery and components.
- Physics Simulations - Moment of inertia is key to modeling rotational dynamics in physical simulations and celestial mechanics.
Accurate calculation of the moment of inertia enhances the safety, efficiency, and performance of engineered and physical systems.
